To down-sample a point cloud, one might decide to keep every second, third, fourth, etc. pixel from the initial, organized point cloud, discarding all other pixels. However, when it comes to a Zivid camera, this is not the best solution. The reason is that our camera sensor has a Bayer filter mosaic. The grid pattern of the Bayer filter mosaic for a 4 x 4 image is shown on the figure below. Each pixel on the camera image corresponds to one color filter on the mosaic. The numbers in the grid pattern represent image coordinates. Note that some image coordinate systems, such as the one in our API, start with (0,0).

Therefore, if a down-sampling algorithm was to keep every other pixel all the pixels would correspond to the same color filter, e.g.:
- (1,1) (1,3) (3,1) (3,3) - blue
- (2,1) (2,3) (4,1) (4,3) - green
- (1,2) (1,4) (3,2) (3,4) - green
- (2,2) (2,4) (4,2) (4,4) - red
To preserve the quality of data, one should consider all pixels while down-sampling a point cloud. In addition, every pixel of the down-sampled image should be obtained based on a procedure performed on an even pixel grid (2x2, 4x4, 6x6, etc.) of the original image. A recommended procedure for down-sampling a Zivid point cloud is described as follows. It is assumed that the goal is to half the point cloud in size by reducing the image from 4x4 to 2x2.
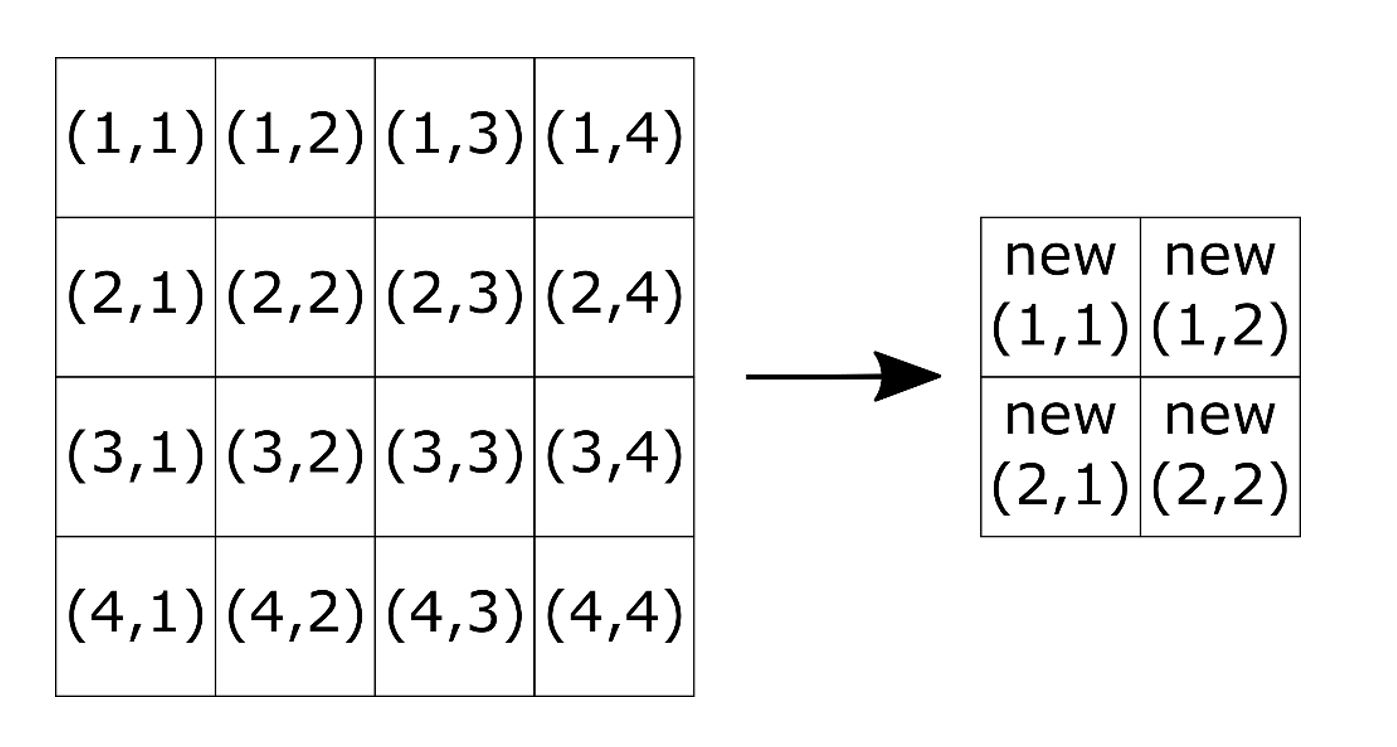
Down-sampling the RGB image
R, G, B pixel values of the new image should be calculated by taking every 2x2 pixel grid of the initial image and calculating the average value for each channel.
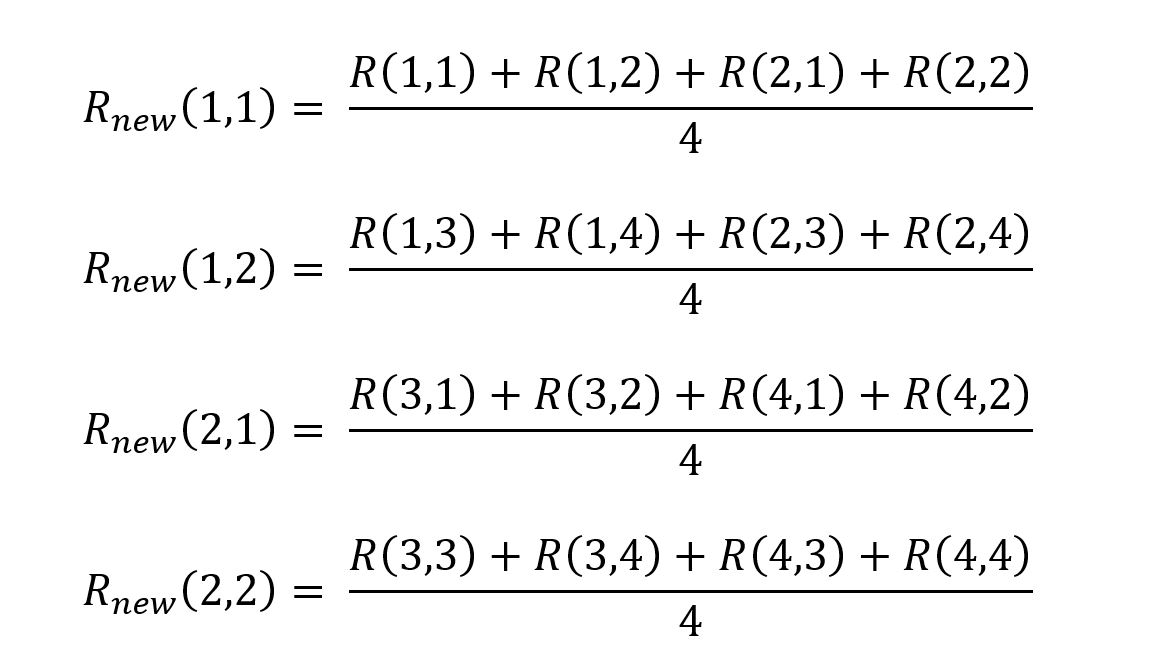
The same should be done for G and B values.
The same procedure that is used to calculate the R, G, B values can be utilized to calculate the X, Y, Z values of the new down-sampled point cloud. However, this is not the best solution and a better approach is described as follows. In addition, X, Y, Z coordinates of any image pixel may have a NaN value, and this is something that needs to be dealt with.
Down-sampling the XYZ values (point cloud)
X, Y, Z pixel values of the new image should be calculated by taking every 2x2 pixel grid of the initial image and calculating the Contrast-weighted average value for each coordinate.
However, X, Y, Z coordinates of any pixel may have a NaN value, while the Contrast for that same pixel may have a value other than NaN. A method to address this is by checking if any pixel has a NaN value for one of the X, Y, Z coordinates, and if it does, replacing the Contrast value for that pixel with zero. This can be done by selecting the pixels whose e.g. Z coordinates are NaNs and setting their Contrast value to zero by:

where is a logical masking function that selects only the pixels whose input coordinates are NaNs.
The next step is calculating the sum of Contrast values for every 2x2 pixel grid.

The next step is calculating the weight for each pixel of the initial image.

To avoid having to deal with instead of it is advisable to do the following:

Finally, X, Y, Z coordinate values can be calculated.
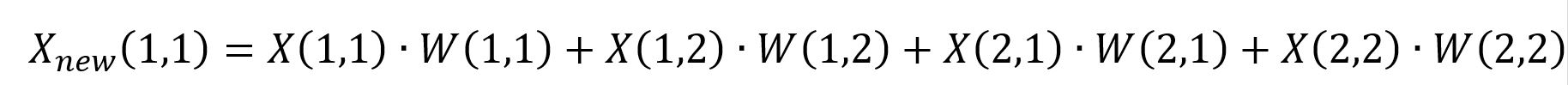
The same should be done for Y and Z values.
Utilizing this approach requires dealing with a) NaN values for X, Y, Z coordinates and b) saturated pixels.
If a pixel is saturated, the Contrast value for that pixel may not be valid. To deal with this, X, Y, Z coordinates of any pixel that has at least one of the R, G, B values equal to 255 should not be taken into consideration; these X, Y, Z coordinates should be replaced with zeroes.
